From the perspective of query processing (QP), aggregation can be both a costly operation, and an operation whose placement has an important impact on query performance.
Aggregation generally computes an aggregated value. Vector aggregation is costly, compared to scalar aggregation, as rows must be grouped together to obtain the aggregated result over a group; this implies, in general, a reordering of the rows through sorting or hashing, both costly operations.
Aggregating after applying cardinality-reducing operators (such as filters) to the input set reduces the cost of aggregation and can thus improve overall query performance.
Aggregating before applying cardinality-increasing operators (such as joins and unions) to the input set reduces the cost of aggregation and can thus improve overall query performance.
Aggregating early can reduce the costs of parent operators through reducing their input set cardinality, and can thus improve overall query performance.
Aggregation can dramatically reduce the cardinality of the input set in the result set, when the grouping columns have relatively few distinct value combinations.
Some properties of the aggregation’s input set, as already grouped (for example, when the aggregation is ordered on the grouping columns), reduce the cost of vector aggregation; in scalar aggregation, rows ordered on the aggregated column allow computing a min or max without accessing each input row.
Plan fragment physical properties have a big impact on aggregation cost.
The naive QP implementation of aggregation places the scalar or vector aggregate operator, as indicated by the SQL query, over the SPJ part of its query block. However, there are algebraic transformations that preserve the semantics of the query and allow aggregation at other places in the operators tree:
Pushing the aggregation down toward the leaves, to aggregate early (called eager aggregation).
Pulling the aggregation up toward the root, to aggregate late (called lazy aggregation).
Plans obtained through such transformations differ greatly in performance. More importantly to distributed query processing (DQP), the cardinality of intermediate results can be greatly reduced by eager aggregation. Such orders-of-magnitude cardinality reduce cross-node data transfer cost, thus removing the main shortcoming of DQP as opposed to traditional QP.
Adaptive Server 15.0.2 and later implements eager aggregation over the leaves of a query plan, which means over the scan operators.
This query illustrates the QP implications of eager aggregation:
select r1, sum(s1) from r,s where r2 = s2 group by r1
Figure 6-1: Typical query execution plan
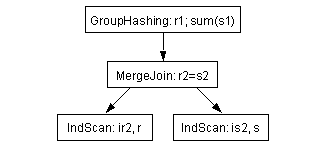
The two index scans, on r(r2) and s(s2) provide the orderings needed by the “r2=s2” merge join. Hash-based grouping is done over the join, as the query specifies it.
The optimizer also generates query plans that perform eager aggregation, also called the push-down of grouping, early grouping, or eager grouping. The SQL representation of the transform using derived tables is:
select r1, sum(sum_s1 * cnt_r) from (select r1, r2, cnt_r = count(*) from r group by r1, r2 ) as gr , (select s2, sum_s1 = sum(s1) from s group by s2 ) as gs where r2 = s2 group by r1
Figure 6-2: Possible eager aggregation plan
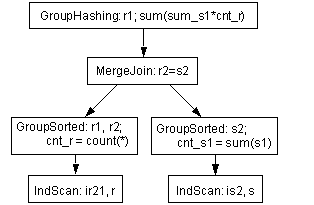
The two eager GroupSorted operators group on the local grouping columns. GroupSorted operators apply to any column projected out for a reason other than that it is an aggregation function argument. These columns include:
The main grouping columns in the group by clause
Columns needed by predicates not yet applied
To place the cheap GroupSorted operator, the child plan fragment must
provide ordering on all the local grouping columns; hence the ir21 index
on r(r2, r1).